题目内容
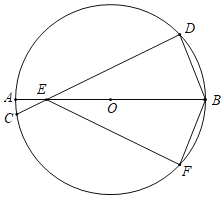
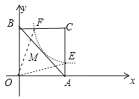
【题目】在平面直角坐标系xOy中,当m,n满足mn=k(k为常数,且m>0,n>0)时,就称点(m,n)为“等积点”.若直线y=﹣x+b(b>0)与x轴、y轴分别交于点A和点B,并且该直线上有且只有一个“等积点”,过点A与y轴平行的直线和过点B与x轴平行的直线交于点C,点E是直线AC上的“等积点”,点F是直线BC上的“等积点”,若△OEF的面积为![]() ,则OE=______.
,则OE=______.
【答案】![]()
【解析】
由题意“等积点”在反比例函数![]() 的图象上,直线y=x+b(b>0)与x轴、y轴分别交于点A和点B,并且直线有且只有一个“等积点”,可得B(0,
的图象上,直线y=x+b(b>0)与x轴、y轴分别交于点A和点B,并且直线有且只有一个“等积点”,可得B(0,![]() ),A(
),A(![]() ,0),E(
,0),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ),“等积点”M的坐标为(
),“等积点”M的坐标为(![]() ,
,![]() ),根据△OEF的面积=S正方形AOBC2S△AOES△EFC=
),根据△OEF的面积=S正方形AOBC2S△AOES△EFC=![]() ,列方程求出k即可解决问题.
,列方程求出k即可解决问题.
解:如图,由题意,“等积点”在反比例函数![]() 的图象上,
的图象上,
∵直线y=x+b(b>0)与x轴、y轴分别交于点A和点B,并且直线上有且只有一个“等积点”,
∴方程![]() 即
即![]() 有两个相等的实数根,
有两个相等的实数根,
∴![]() ,即
,即![]() ,
,
∴B(0,![]() ),A(
),A(![]() ,0),E(
,0),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ),“等积点”M
),“等积点”M![]() ,
,![]() ),
),
∵△OEF的面积=S正方形AOBC2S△AOES△EFC=![]() ,
,
∴![]() ,
,
解得:k=2或![]() (舍弃),
(舍弃),
∴E(![]() ,
,![]() ),
),
∴OE=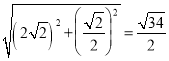 ,
,
故答案为:![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.两个厂家销售情况如下表:
甲厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 2 | 4 | 2 | 1 | 1 |
乙厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 1 | 2 | 2 | 4 | 1 |
(1)现从乙厂家试销的10天中随机抽取1天,求这1天的返利不超过160元的概率;
(2)商场拟甲、乙两个厂家中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.