题目内容
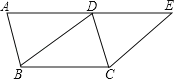
【题目】△ABC与△ADE都是等腰直角三角形,且AC=AB,AD=AE,连接DC,点M、P、N分别为DE、DC、BC的中点.

(1)如图1,当点D、E分别在边AB、AC上,线段PM与PN的数量关系是 ,位置关系是 ;
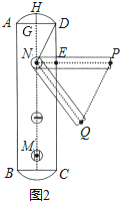
(2)把等腰Rt△ADE绕点A旋转到如图2的位置,连接MN,判断△PMN的形状,并说明理由;
(3)把等腰Rt△ADE绕点A在平面内任意旋转,AD=2,AB=6,请直接写出△PMN的面积S的变化范围 .
【答案】(1)PM=PN,PM⊥PN;(2)△PMN是等腰直角三角形,见解析;(3)2≤S≤8
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出结论;
BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=14,再判断出B
最小时,△PMN最小,即可得出结论.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
(2)△PMN是等腰直角三角形.
由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位线得,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形;
(3)由(2)知,△PMN是等腰直角三角形,PM=PN=![]() BD,
BD,
∴PM最大时,△PMN面积最大,PM最小时,△PMN面积最小
∴点D在BA的延长线上,△PMN的面积最大,
∴BD=AB+AD=8,
∴PM=4
∴S最大=![]() PM2=
PM2=![]() ×42=8,
×42=8,
当点D在线段AB上时,△PMN的面积最小,
∴BD=AB﹣AD=4,
∴PM=2,
S最小=![]() PM2=
PM2=![]() ×22=2,
×22=2,
∴2≤S≤8,
故答案为:2≤S≤8.

 阅读快车系列答案
阅读快车系列答案