题目内容
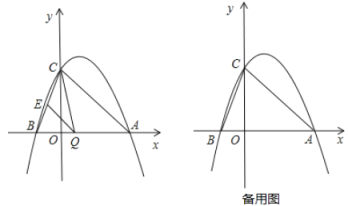
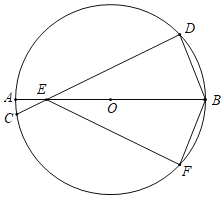
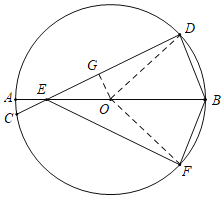
【题目】如图所示,⊙O的直径AB和弦CD相交于点E,且点B是劣弧DF的中点.
(1)求证:△EBD≌△EBF;
(2)已知AE=1,EB=5,∠DEB=30°,求CD的长.
【答案】(1)见解析;(2)CD=4![]()
【解析】
(1)连接OD、OF,,根据等弧所对的弦相等,可得BD=BF,再根据弧与圆周角的关系可得∠DBE=∠EBF,利用SAS可得结论;
(2)先由AE=1,EB=5,得到半径OB=3,则OE=2,在Rt△EFO中,利用含30度的直角三角形三边的关系得到OG的长,根据勾股定理可计算DG的长,从而得CD的长.
解:(1)连接OD、OF,
∵B是劣弧DF的中点,
∴![]() ,
,
∴![]() ,
,
∴BD=BF,∠DBE=∠EBF,
在△EBD和△EBF中,
∵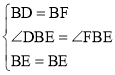 ,
,
∴△EBD≌△EBF(SAS);
(2)∵AE=1,EB=5,
∴AB=6,
∵AB是⊙O的直径,
∴OD=OA=3,OE=3﹣1=2,
过O作OG⊥CD于G,则CD=2DG,
∵∠DEB=30°,∠EGO=90°,
∴OG=![]() OE=1,
OE=1,
由勾股定理得:DG=![]() =
=![]() =2
=2![]() ,
,
∴CD=2DG=4![]() .
.

练习册系列答案
相关题目