题目内容
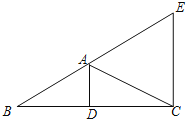
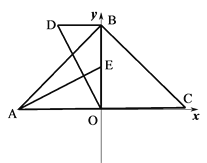
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=α.



(1)当α=60°, 如图则,∠DPE的度数______________
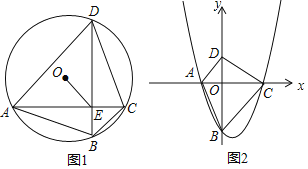
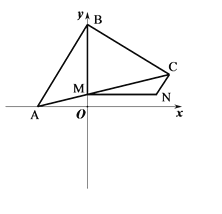
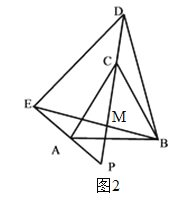
(2)若△BDE绕点B旋转一定角度,如图所示,求∠DPE(用α表示)
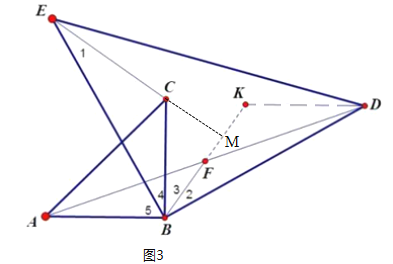
(3)当α=90°,其他条件不变,F为AD的中点,求证 :EC ⊥ BF
【答案】(1)60°;(2)α;(3)证明见解析.
【解析】
(1)由SAS证明△ABE≌△CBD,得到∠AEB=∠CDB,再由对顶角相等及三角形内角和公式可得∠EPD=∠EBD即可;
(2)与(1)同理可求∠DPE=∠DBE,即可得出结论;
(3)延长BF到K,使FK=BF,连接KD,延长EC交BK于M.由SAS证明△AFB≌△DFK,得到AB=KD,∠ABF=∠DKF,进而得到BC=KD,KD∥AB,再证明∠BDK=∠4,得到△EBC≌△BDK,由全等三角形对应角相等得到∠1=∠2,即可得出结论.
(1)如图1,设BE和CD相交于M.
∵∠ABC=∠DBE,∴∠ABE=∠CBD.
在△ABE和△CBD中,∵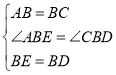 ,∴△ABE≌△CBD(SAS),∴∠AEB=∠CDB.
,∴△ABE≌△CBD(SAS),∴∠AEB=∠CDB.
在△PME和△BMD中,∵∠PME=∠BMD,∠AEB=∠CDB,∴∠EPD=180°-∠AEB-∠PME=180°-∠CDB-∠BMD=∠MBD=60°;
(2)如图2,同理可求∠DPE=∠DBE=α;
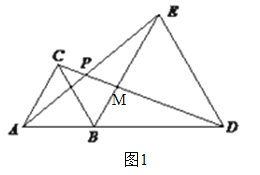
(3)如图3,延长BF到K,使FK=BF,连接KD,延长EC交BK于M.
∵AF=DF,∠AFB=∠DFK,BF=KF,∴△AFB≌△DFK,∴AB=KD,∠ABF=∠DKF,∴BC=KD,KD∥AB,∴∠BDK+∠ABD=180°,∴∠BDK=180°-∠ABD=180°-(∠2+∠3+∠4+∠5)=180°-[(90°-∠4)+90°]=∠4.
在△EBC和△BDK中,∵EB=BD,∠4=∠BDK,BC=DK,∴△EBC≌△BDK,∴∠1=∠2.
∵∠2+∠EBK=90°,∴∠1+∠EBK=90°,∴∠EMB=90°,∴EC⊥BF.