Question

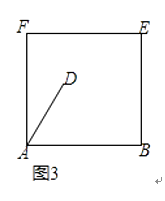
【题目】如图，BD为矩形ABCD的对角线，AE⊥BD，垂足为E，tan∠BAE= ，BE=1，点P、Q分别在BD、AD上，连接AP、PQ，则AP+PQ的最小值为 ．

Answer 1

【答案】3
【解析】解：

∵四边形ABCD为矩形，且AE⊥BD，tan∠BAE= ，BE=1，

∴AB=2，AE= ，

∵tan∠BAE= ，

∴∠BAE=30°，

∴∠EAD=60°，

∵AE= ，

∴DE=3，

如图，设A点关于BD的对称点为A′，连接A′D，PA′，

则A′A=2AE=2 ，AD=A′D=2 ，

∴△AA′D是等边三角形，

∵PA=PA′，

∴当A′、P、Q三点在一条线上时，A′P+PQ最小，

又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，

∴AP+PQ=A′P+PQ=A′Q=DE= ，

所以答案是： ．

【考点精析】认真审题，首先需要了解轴对称-最短路线问题(已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径)．