题目内容
【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.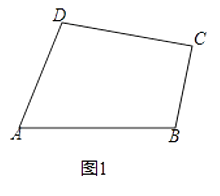
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.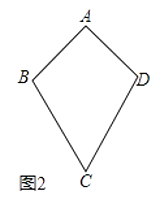
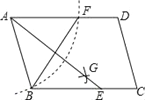
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.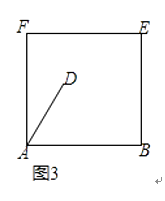
【答案】
(1)证明:∵在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.
∴∠D=360°﹣∠A﹣∠B﹣∠C=100°,∠A≠∠C,
∴∠D=∠D,
∴四边形ABCD是“等对角四边形”
(2)证明:如图2,连接BD,
∵AB=AD,CB=CD,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∴∠ABD+∠CBD=∠ADB+∠CDB,
∴∠ABC=∠ADC,
∵AB=AD=a,CB=CD=b,且a≠b,且BD=BD,
∴△ABD与△CBD不相似,
∴∠A≠∠C,
∴四边形ABCD是“等对角四边形”
(3)如图3,连接BD,
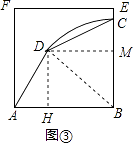
当∠DAB=∠BCD=60°时,四边形ABCD是“等对角四边形”,
此时点C在BD为弦的 ![]() 上,
上,
要使四边形ABCD的面积最大,则点C在边BE上,
过点D作DH⊥AB于点H,作DM⊥BC于点M,
在Rt△ADH中,∠DAH=60°,AD=4,
∴AH=2,DH=2 ![]() ,
,
∴BH=AB﹣AH=4,
∵四边形DHBM是矩形,
∴BM=DH=2 ![]() ,DM=BH=4,
,DM=BH=4,
在Rt△DMC中,∠DCM=60°,
∴CM= ![]() DM=
DM= ![]() ,
,
∴BC=BM+CM=2 ![]() +
+ ![]() =
= ![]() ,
,
∴S四边形ABCD=S△ABD+S△BCD= ![]() ×6×2
×6×2 ![]() +
+ ![]() ×
× ![]() ×4=
×4= ![]() (m2)
(m2)
【解析】(1)求出第4个角度数,按照定义即可判断出结论;(2)利用等边对等角定理,须连接BD,得出有一组对角相等,再证另一组对角不等,得出结论;(3)借鉴(2)的方法,要使∠BCD=60°,C需在以BD为弦的弧BD上,若四边形ABCD的面积最大,则点C在边BE上,才能使高最大,进而面积最大.
【考点精析】掌握三角形的面积和圆周角定理是解答本题的根本,需要知道三角形的面积=1/2×底×高;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案