题目内容
【题目】如图（1），抛物线W1：y=﹣x2+4x与x轴的正半轴交于点B，顶点为A，抛物线W2与W1关于x轴对称，顶点为D．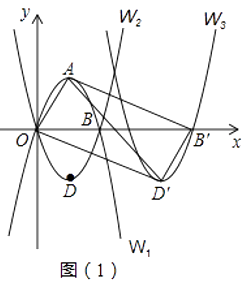
（1）求抛物线W2的解析式；
（2）将抛物线W2向右平移m个单位，点D的对应点为D′，点B的对应点为B′，则当m为何值时，四边形AOD′B′为矩形？请直接写出m的值．
（3）在（2）的条件下，将△AOD′沿x轴的正方向向右平移n个单位（0＜n＜5），得到△A′O′D′′，AD′分别与O′A′、O′D′′交于点M、点P，A′D′′分别与AB′、B′D′交于点N、点Q．
①求当n为何值时，四边形MNQP为菱形？
②若四边形MNQP的面积为S，求S关于n的函数关系式；并求当n为何值时，S的值最大？最大值为多少？
【答案】
（1）解：由y=﹣x2+4x=﹣（x﹣2）2+4得，点A坐标为（2，4），
∵抛物线W2与W1关于x轴对称，
∴点D坐标为（2，﹣4），
∴抛物线W2的解析式为y=（x﹣2）2﹣4，即y=x2﹣4x
（2）解：∵点A坐标为（2，4），
∴直线OA=2x，
∵点D坐标为（2，﹣4），
∴D′（2+m，﹣4），
∴直线OD′的解析式为y=﹣ 
x，
∵四边形AOD′B′为矩形，
∴AO⊥OD′，
∴2×（﹣ ）=﹣1，
∴m=6，
∴当m的值为6时，四边形AOD′B′为矩形
（3）解：①当y=0时，﹣x2+4x=0，解得x1=0，x2=4．
∴点B坐标为（4，0），
又∵m=6，
∴B′坐标为（10，0），
∴OB′=10；
设矩形AOD′B′的对角线AD′与OB′交于点E，A′D′′与x轴交于点F．．
∵四边形AOD′B′为矩形，
∴AE=OE=B′E=D′E=5，
∴∠OAE=∠AOE，∠EOD′=∠DOE．
∵A′O′∥AO，O′D′′∥OD′，
∴∠EMO′=∠MO′E，∠EO′P=∠EPO′，
∴ME=EO′=EP，
∵OE=5，OO′=n，
∴O′E=5﹣n，
∴ME=EP=5﹣n．
同理NF=FQ=FB′=5﹣n．
∵MP∥NQ，
∴四边形MEFN，EPQF为平行四边形．
∴MN∥EF∥PQ，
∴四边形MNQP为平行四边形，
∴当MN=MP时，四边形MNQP为菱形．
∵MN=AA′=n，MP=2O′E=10﹣2n．
∴n=10﹣2n．
解得n= 
．
∴当n= 时，四边形MNQP为菱形；
②过M作MH⊥x轴，垂足为H，过A作AG⊥x轴，垂足为G，
则△MHE∽△AGE，
∴ 
，
∴ 
= 
，
∴MH= （5﹣n），
∴S=2S□MEFN=2× （5﹣n）﹣n=﹣ 
n2+8n，
∵S=﹣ （n﹣ 
）2+10，∵﹣ ＜0，
∴当n= 时，S的值最大，最大值为10．
【解析】（1）抛物线关于x 轴对称与点的对称类似，横坐标不变，纵坐标变为其相反数，即-y=﹣x2+4x,y=x2-4x;（2）先求OA解析式，再用m的代数式表示直线OD′的解析式，根据矩形的性质，得出二直线互相垂直，即斜率之积为-1，求出m；（3）由已知可得四边形MNQP为平行四边形，若四边形MNQP为菱形须MN=MP，构建n的方程n=10﹣2n，求出ｎ；最值问题可运用函数思想，构建Ｓ关于ｎ的函数，二次函数可配成顶点式，求出最值．
