题目内容
【题目】二次函数y=x2+x+c的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m,n)是图象上一点,那么下列判断正确的是( )
A.当n<0时,m<0
B.当n>0时,m>x2
C.当n<0时,x1<m<x2
D.当n>0时,m<x1
【答案】C
【解析】解:∵a=1>0,
∴开口向上,
∵抛物线的对称轴为:x=﹣![]() ,
,
二次函数y=x2+x+c的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),且x1<x2 ,
无法确定x1与x2的正负情况,
∴当n<0时,x1<m<x2 , 但m的正负无法确定,故A错误,C正确;
当n>0时,m<x1 或m>x2 , 故B,D错误,
故选C.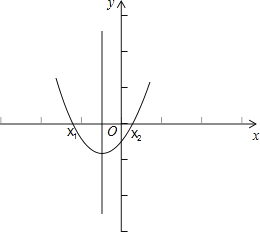
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

【题目】在天水市汉字听写大赛中,10名学生得分情况如表
人数 | 3 | 4 | 2 | 1 |
分数 | 80 | 85 | 90 | 95 |
那么这10名学生所得分数的中位数和众数分别是( )
A.85和82.5
B.85.5和85
C.85和85
D.85.5和80
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.