题目内容
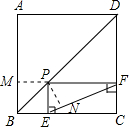
如图，在梯形ABCD中，AD∥BC，∠A=90°，E是边AB上一点，且BE=AD，F是CD的中点，EF⊥CD．求证：AE=BC．
证明：∵F是CD的中点，EF⊥CD，
∴直线EF时CD的垂直平分线，
∴ED=EC，
在△ADE与△BEC中
∵AD∥BC，
∴∠B=∠A=90°，
∵BE=AD，
∴Rt△ADE≌Rt△BEC（HL），
∴AE=BC．
∴直线EF时CD的垂直平分线，
∴ED=EC，
在△ADE与△BEC中
∵AD∥BC，
∴∠B=∠A=90°，
∵BE=AD，
∴Rt△ADE≌Rt△BEC（HL），
∴AE=BC．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
