Question

有若干个边长都为2的小正方形．若小正方形Ⅱ的一个顶点在小正方形I的中心O₁，如图所示；类似地小正方形Ⅲ的一个顶点在小正方形Ⅱ的中心O₂，并且小正方形I与小正方形Ⅲ不相重叠，如果若干个小正方形都按这种方法拼接，问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积，并给出你的证明过程．

Answer 1

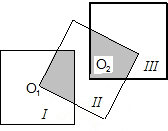
需要5个小正方形能使拼接出的图形的阴影部分面积等于一个小正方形的面积．理由如下：
对于正方形Ⅰ与正方形Ⅱ，
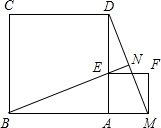
过O₁作正方形的边AN、MN的垂线O₁F、O₁E，垂足分别为F、E，连接O₁N、O₁M．
∵O₁为正方形Ⅰ的中心，
∴O₁N=O₁M，∠O₁NC=∠O₁MD=45°，∠NO₁M=90°，
S_△NO1M=

1

4

S_正方形1，
∵∠CO₁N+∠NO₁D=∠CO₁D=90°，∠DO₁M+∠NO₁D=∠NO₁M=90°，
∴∠CO₁N=∠DO₁M．
在△NCO₁与△MDO₁中，
∵

∠O1NC=∠O1MD O1N=O1M ∠CO1N=∠DO1M

，
∴△NCO₁≌△MDO₁（ASA），
∴S△NCO1=S△MDO1，
∴S_{四边形NCO1D}=S_△NO1M，
即正方形Ⅰ与正方形Ⅱ重合部分的阴影部分面积为正方形面积的

1

4

，
∴需要5个小正方形能使拼接出的图形的阴影部分面积等于一个小正方形的面积．