题目内容
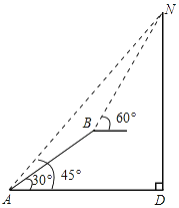
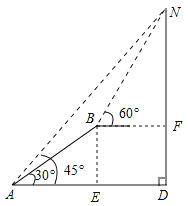
【题目】如图，小明在山脚下的A处测得山顶N的仰角为45°，此时，他刚好与山底D在同一水平线上．然后沿着坡度为30°的斜坡正对着山顶前行110米到达B处，测得山顶N的仰角为60°．求山的高度．（结果精确到1米，参考数据： 
≈1.414， 
≈1.732）．
【答案】山的高度为150米．
【解析】
试题过点B作BF⊥DN于点F，过点B作BE⊥AD于点E，即可得四边形BEDF是矩形，根据矩形的性质可得BE=DF，BF=DE，在Rt△ABE中，根据锐角三角函数可求得AE、BE的长，设BF=x米，则AD=AE+ED=55
+x米，在Rt△BFN中，用x表示NF的长，利用AD=DN列出方程即可解答．
试题解析：
过点B作BF⊥DN于点F，过点B作BE⊥AD于点E，
∵∠D=90°，
∴四边形BEDF是矩形，
∴BE=DF，BF=DE；
在Rt△ABE中，AE=ABcos30°=110×
=55（米）
BE=ABsin30°=
×110=55（米）
设BF=x米，则AD=AE+ED=55+x（米），
在Rt△BFN中，NF=BFtan60°=x（米），
∵∠NAD=45°，
∴AD=DN，
∴DN=DF+NF=55+x（米），
即55+x=x+55，
解得：x=55，
∴DN=55+
x≈150（米）．
答：山的高度为150米．
练习册系列答案
相关题目
