Question

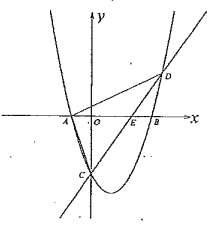
【题目】在平面直角坐标系xOy中，抛物线y＝mx2﹣2mx+n(m≠0)与x轴交于点A，B，点A的坐标为(﹣2，0)．

(1)写出抛物线的对称轴；

(2)直线过点B，且与抛物线的另一个交点为C．

①分别求直线和抛物线所对应的函数表达式；

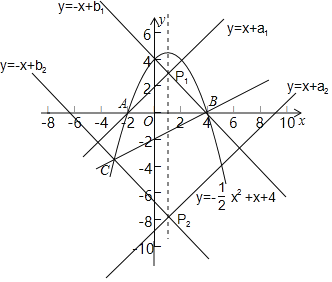
②点P为抛物线对称轴上的动点，过点P的两条直线l1：y＝x+a和l2：y＝﹣x+b组成图形G．当图形G与线段BC有公共点时，直接写出点P的纵坐标t的取值范围．

Answer 1

【答案】（1）抛物线的对称轴为直线x＝1；（2）①直线所对应的函数表达式为，抛物线所对应的函数表达式为；②

【解析】

（1）由给定的抛物线的表达式，利用二次函数的性质即可找出抛物线的对称轴；

（2）①根据抛物线的对称性可得出点B的坐标，再利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征，即可求出m、n的值，此问得解；

②联立直线及抛物线的函数关系式成方程组，通过解方程组可求出点C的坐标，利用一次函数图象上点的坐标特征求出直线l2过点B、C时b的值，进而可得出点P的坐标，再结合函数图象即可找出当图形G与线段BC有公共点时，点P的纵坐标t的取值范围．

（1）∵抛物线所对应的函数表达式为y＝mx2﹣2mx+n，

∴抛物线的对称轴为直线x＝﹣＝1．

（2）①∵抛物线是轴对称图形，

∴点A、B关于直线x＝1对称．

∵点A的坐标为（﹣2，0），

∴点B的坐标为（4，0）．

∵抛物线y＝mx2﹣2mx+n过点B，直线y＝x﹣4m﹣n过点B，

∴，

解得：，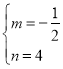

∴直线所对应的函数表达式为，抛物线所对应的函数表达式为．

②联立两函数表达式成方程组，，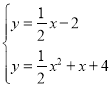

解得：，．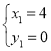

∵点B的坐标为（4，0），

∴点C的坐标为（﹣3，﹣）．

当直线l2：y＝﹣x+b1过点B时，0＝﹣4+b1，

解得：b1＝4，

∴此时直线l2所对应的函数表达式为y＝﹣x+4，

当x＝1时，y＝﹣x+4＝3，

∴点P1的坐标为（1，3）；

当直线l2：y＝﹣x+b2过点C时，﹣＝3+b2，

解得：b2＝﹣，

∴此时直线l2所对应的函数表达式为y＝﹣x﹣，

当x＝1时，y＝﹣x﹣＝﹣，

∴点P2的坐标为（1，﹣）．

∴当图形G与线段BC有公共点时，点P的纵坐标t的取值范围为