Question

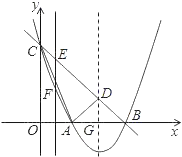
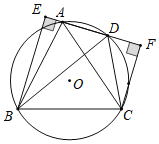
【题目】如图，⊙O是正△ABC的外接圆，点D为圆上一点，连接AD，分别过点B和点C作AD延长线的垂线，垂足分别为点E和点F，连接BD、CD，已知EB=3，FC=2，现在有如下4个结论：①∠CDF=60°；②△EDB∽△FDC；③BC=；④，其中正确的结论有（　　）个

A. 1

B. 2

C. 3

D. 4

Answer 1

【答案】B

【解析】

根据等边三角形的性质，相似三角形的判定和性质，解直角三角形等知识一一判断即可．

解：∵△ABC是等边三角形

∴∠ABC=∠ACB=∠BAC=60°，

∵A、B、C、D四点共圆，

∴∠CDF=∠ABC=60°，故①正确．

∵∠BDE=∠ACB=60°，

∴∠BDE=∠CDF=60°，

∵BE⊥AD，CF⊥AD，

∴∠E=∠F=90°，

∴△EDB∽△FDC，故②正确．

∵BE=DE=3，CF=DF=2，

∴DE=，DF=，

∴EF=DE+DF=． 过点C作CG⊥BE于点G．

∴四边形EGCF是矩形，

∴EG=FC=2，CG=EF=，

∴BG=BE-EG=1．

在Rt△BGC中，由勾股定理可得：BC=，故③错误．

在Rt△AEB中，由勾股定理可得：AE=，

∴AD=DE-AE=，

∴AD：DE=2：3．

∴S△ADB=S△EDB，故④错误．

故选：B．