题目内容
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
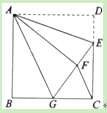
![]()
【答案】C
【解析】①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;
②正确.因为:EF=DE=![]() CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.
过F作FH⊥DC,
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴![]() =
=![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴![]() =
=![]() =
=![]() ,
,
∴S△FGC=S△GCE﹣S△FEC=![]() ×3×4﹣
×3×4﹣![]() ×4×(
×4×(![]() ×3)=
×3)=![]() ≠3.
≠3.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目