题目内容
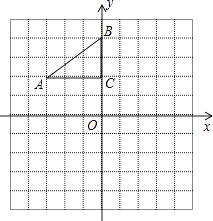
【题目】为了考察冰川的融化状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km的圆形考察区域，线段P1P2是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动，若经过n年，冰川的边界线P1P2移动的距离为s（km），并且s与n（n为正整数）的关系是s= 
n2﹣ 
n+ 
．以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别为（﹣4，9）、（﹣13、﹣3）． 
（1）求线段P1P2所在直线对应的函数关系式；
（2）求冰川边界线移动到考察区域所需的最短时间．
【答案】
（1）解：设P1P2所在直线对应的函数关系式是y=kx+b，根据题意，得
，
解得：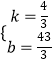 
，
∴直线P1P2的解析式是：y= 
x+ 
；
（2）解：在y= x+ 中，
当x=0，则y= ，
当y=0，则x=﹣ 
，
∴与x、y轴的交点坐标是（0， ）、（﹣ ，0）．
由勾股定理，得 
= 
，
当P1P2与⊙O相切时，此时冰川移动的距离最短，
设移动的最短距离是s，O点到直线P1P2的距离为x，
则根据面积相等列出等式， 
× × = × x，
解得：x= 
，
即s= ﹣4= 
∵s= 
n2﹣ 
n+ 
，
∴ n2﹣ n+ = ，
解得：n1=6，n2=﹣4.8（舍去）
答：冰川边界线移动到考察区域所需的最短时间为6年．
【解析】（1）设P1P2所在直线对应的函数关系式是y=kx+b，由待定系数法求出其解就可以得出结论；（2）由（1）的解析式求出直线P1P2与坐标轴的交点，设最短距离为a，由三角形的面积相等建立方程，求出a的值就求出了s的值，再代入s= n2﹣ n+ 就可以求出时间．
【题目】某小商场以每件20元的价格购进一种服装，先试销一周，试销期间每天的销量（件）与每件的销售价x（元/件）如下表：
x（元/件） | 38 | 36 | 34 | 32 | 30 | 28 | 26 |
t（件） | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
假定试销中每天的销售量t（件）与销售价x（元/件）之间满足一次函数．
（1）试求t与x之间的函数关系式；
（2）在商品不积压且不考虑其它因素的条件下，每件服装的销售定价为多少时，该小商场销售这种服装每天获得的毛利润最大？每天的最大毛利润是多少？（注：每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价）
