题目内容
如图,已知点A在反比例函数y=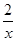 的图象上,点B,C分别在反比例函数y=
的图象上,点B,C分别在反比例函数y=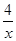 的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为( )
的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为( )

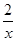 的图象上,点B,C分别在反比例函数y=
的图象上,点B,C分别在反比例函数y=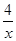 的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为( )
的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为( )
(2,1)
首先设A(x,y),根据AB∥x轴,AC∥y轴,则可设B(a,y),C(x,y+AC),再根据A、B点所在图象的函数关系式得到a=2x,再算出AB的长,再由条件AB=2AC得到AC的长,进而表示出C点坐标,再根据C在反比例函数y=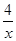 的图象上,可算出x的值,即可得到A点坐标.
的图象上,可算出x的值,即可得到A点坐标.

解:设A(x,y),
∵AB∥x轴,AC∥y轴
∴B(a,y),C(x,y+AC),
∵A在反比例函数y=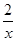 的图象上,
的图象上,
∴xy=2,
∵点B在反比例函数y=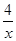 的图象上,
的图象上,
∴ay=4,
∴a=2x,
则AB=2x-x=x,
∵AB=2AC,
∴AC= x,
x,
∴C(x, x+y),
x+y),
∵C在反比例函数y=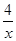 的图象上,
的图象上,
∴x×( x+y)=4,
x+y)=4,
 x2+xy=4,
x2+xy=4,
 x2+2=4,
x2+2=4,
解得:x=±2,
∵A在第一象限,
∴x=2,
则y=1,
∴A(2,1),
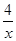 的图象上,可算出x的值,即可得到A点坐标.
的图象上,可算出x的值,即可得到A点坐标.
解:设A(x,y),
∵AB∥x轴,AC∥y轴
∴B(a,y),C(x,y+AC),
∵A在反比例函数y=
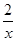 的图象上,
的图象上,∴xy=2,
∵点B在反比例函数y=
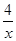 的图象上,
的图象上,∴ay=4,
∴a=2x,
则AB=2x-x=x,
∵AB=2AC,
∴AC=
 x,
x,∴C(x,
 x+y),
x+y),∵C在反比例函数y=
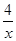 的图象上,
的图象上,∴x×(
 x+y)=4,
x+y)=4, x2+xy=4,
x2+xy=4, x2+2=4,
x2+2=4,解得:x=±2,
∵A在第一象限,
∴x=2,
则y=1,
∴A(2,1),

练习册系列答案
相关题目
 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;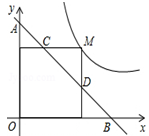

 B.
B.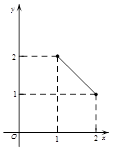 C.
C.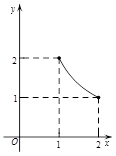 D.
D.
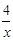 (x>0)的图像上,点B在反比例函数y=-
(x>0)的图像上,点B在反比例函数y=-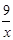 (x<0)的图像上,且 ∠AOB=90°,则tan∠OAB ( ).
(x<0)的图像上,且 ∠AOB=90°,则tan∠OAB ( ).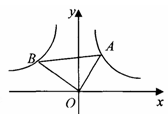
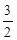

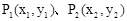 在双曲线
在双曲线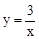 上,若
上,若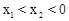 ,则
,则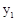
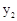 (用“>”或“<”或“=”号表示).
(用“>”或“<”或“=”号表示).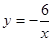 和
和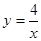 的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )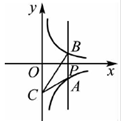
 的图象经过第二、四象限,则k的取值范围是________.
的图象经过第二、四象限,则k的取值范围是________.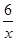 的图象,并根据图象回答问题.
的图象,并根据图象回答问题.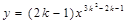 的图象位于第二、四象限,则
的图象位于第二、四象限,则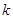 的值是( )
的值是( )