题目内容
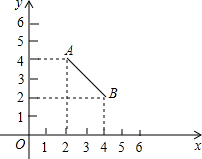
在如图所示的平面直角坐标系中,已知点A(2,4),B(4,2).
(1)在平面直角坐标系中,我们把横坐标、纵坐标都为整数的点称为整数点,请在第一象限内求作一个整数点C,使得AC=BC,且AC的长为小于4的无理数,则C点的坐标是______,△ABC的面积是______;
(2)试求出△ABC外接圆的半径.
(1)在平面直角坐标系中,我们把横坐标、纵坐标都为整数的点称为整数点,请在第一象限内求作一个整数点C,使得AC=BC,且AC的长为小于4的无理数,则C点的坐标是______,△ABC的面积是______;
(2)试求出△ABC外接圆的半径.

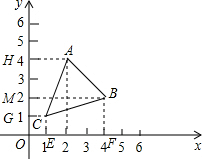
(1)作AB的垂直平分线,从图形中可以看出C点的坐标是C1(1,1),C2(5,5)
过A作AH⊥Y轴于H,过B作BM⊥Y轴于M,BF⊥X轴于F,过C作CG⊥Y轴于G,CE⊥X轴于E,
当C1(1,1)时,S△ABC=S梯形AHMB+S矩形BMOF-S梯形AHGC-S正方形OGCE-S梯形CEFB,
=
×(2+4)×2+4×2-
×(1+2)×(4-1)-1×1-
×(1+2)×(4-1),
=4;
当C2(5,5)时,同法可求S△ABC=4;
故答案为:(1,1)和(5,5),4.
(2)如图,在△ABC中,作CD⊥AB于D,连接AE,E为圆心,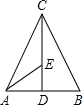
∵由勾股定理得:AC=BC=
,AB=2
,
∴CD=2
,
设半径AE=CE=x,则x2=(
)2+(2
-x)2,
∴半径x=
.
答:△ABC外接圆的半径是
.
过A作AH⊥Y轴于H,过B作BM⊥Y轴于M,BF⊥X轴于F,过C作CG⊥Y轴于G,CE⊥X轴于E,
当C1(1,1)时,S△ABC=S梯形AHMB+S矩形BMOF-S梯形AHGC-S正方形OGCE-S梯形CEFB,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4;
当C2(5,5)时,同法可求S△ABC=4;
故答案为:(1,1)和(5,5),4.
(2)如图,在△ABC中,作CD⊥AB于D,连接AE,E为圆心,

∵由勾股定理得:AC=BC=
| 10 |
| 2 |
∴CD=2
| 2 |
设半径AE=CE=x,则x2=(
| 2 |
| 2 |
∴半径x=
| 5 |
| 4 |
| 2 |
答:△ABC外接圆的半径是
| 5 |
| 4 |
| 2 |


练习册系列答案
相关题目