题目内容
【题目】如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确有()个.

① SA+SB+SC+SD=49;② SE+SF=49;③ SA+SB+SF=49;④ SC+SD+SE=4
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
如下图,根据勾股定理得a2+b2=e2、c2+d2=f2、e2+f2=g2,即a2+b2+c2+d2 =g2即可解题.
解:如下图,设正方形的边长分别为a、b、c、d、e、f、g,
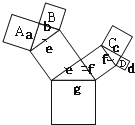
根据正方形的面积公式等于边长的平方,
∴四边形A的面积是a2,四边形B的面积是b2,
a、b是对应直角三角形的直角边,根据勾股定理,则有a2+b2=e2;
同理,四边形C的面积是c2,四边形D的面积是d2,
c、d是对应直角三角形的直角边,根据勾股定理,则有c2+d2=f2;
根据正方形的对边相等,e、f就是下面大直角三角形的直角边,根据勾股定理,得到e2+f2=g2,
∵g是最大的正方形边长为7cm,
∴正方形A、B、C、D面积之和为7×7=49平方厘米.

练习册系列答案
相关题目