题目内容
如图,正方形ABCD,点E、F分别为BC、CD边上的点,连接EF,点 M为EF上一点,且使AE平分∠BAM,AF平分∠DAF, 证明:∠EAF=45°

45°
试题分析:证明:∵正方形ABCD
∴∠BAD=90°
∵ AE平分∠BAM,AF平分∠DAF
∴∠EAM=
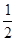 ∠BAM,∠MAF=
∠BAM,∠MAF=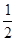 ∠DAM
∠DAM ∴
 ∠EAM+∠MAF=
∠EAM+∠MAF=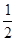 ∠BAM+
∠BAM+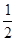 ∠DAM
∠DAM=
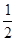 (∠BAM+∠DAM)
(∠BAM+∠DAM)=
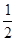 ∠BAD=
∠BAD=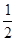 ×90°=45°
×90°=45° 即∠EAF=∠EAM+∠MAF=45°
点评:本题难度中等,主要考查学生对正方形和三角形性质的掌握和综合运用性质定理的能力。为中考常考题型。

练习册系列答案
相关题目

 cm B.
cm B. cm
cm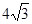 cm D.3 cm
cm D.3 cm 的位置如图所示,点
的位置如图所示,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ;延长
;延长 交
交 轴于点
轴于点 ,作正方形
,作正方形 ;延长
;延长 交
交 ,作正方形
,作正方形 …;按这样的规律进行下去,第
…;按这样的规律进行下去,第 个正方形的面积为
个正方形的面积为



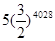

 中,
中, ,
, ,
, ,
, ,
, 为
为 上一动点,则
上一动点,则 周长的最小值为 .
周长的最小值为 .

 ,
, ,
,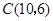 ,
, ,直线
,直线 将四边形
将四边形 分成面积相等的两部分,则
分成面积相等的两部分,则 的值为 .
的值为 . 边形的内角和为1260°,则
边形的内角和为1260°,则