题目内容
【题目】已知抛物线![]()
(1)证明:不论m为何值,抛物线图象的顶点![]() 均在某一直线
均在某一直线![]() 的图象上,求此直线
的图象上,求此直线![]() 的函数解析式;
的函数解析式;
(2)当![]() 时,点P为抛物线上一点,且
时,点P为抛物线上一点,且![]() ,求点P的坐标;
,求点P的坐标;
(3)将(2)中的抛物线![]() 沿x轴翻折再向上平移1个单位向右平移
沿x轴翻折再向上平移1个单位向右平移![]() 个单位得抛物线
个单位得抛物线![]() ,设抛物线
,设抛物线![]() 的顶点为
的顶点为![]() ,抛物线
,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() (A在B的左边),且
(A在B的左边),且![]() ∥
∥![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用配方法可确定抛物线的顶点M坐标为(m-1,-m-2),然后令x=m-1,y=-m-2,然后消去m得到x和y的关系式即可;
(2)先确定抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),利用旋转的定义,将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,从而得到点C坐标,再求出直线OP的解析式为y=![]() x,然后解方程组
x,然后解方程组 得P点坐标;
得P点坐标;
(3)利用抛物线的几何变换得到N(n+1,5),抛物线C2的解析式为y=-(x-n-1)2+5,过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,根据抛物线与x轴的交点问题求出A点和B点坐标,然后证明Rt△AME∽Rt△BNF,再利用相似比得到关于n的方程,解方程可得到n的值.
试题解析:(1)证明:y=x2-2(m-1)x+m2-3m-1=[x-(m-1)]2-m-2,则抛物线的顶点M坐标为(m-1,-m-2),
令x=m-1,y=-m-2,
则x+y=-3,
所以直线l的函数解析式为y=-x-3;
(2)当m=2时,抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),
将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,

则点C坐标为(4,1),设直线OC的解析式为y=kx,
把C(4,1)代入得4k=1,解得k=![]() ,
,
所以直线OP的解析式为y=![]() x,
x,
解方程组 得
得 或
或 ,
,
所以点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)由题意可知,抛物线C2的顶点N(n+1,5),则抛物线C2的解析式为y=-(x-n-1)2+5,
过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,

当y=0时,-(x-n-1)2+5=0,解得x1=n+1-![]() ,x2=n+1+
,x2=n+1+![]() ,
,
∴A(n+1-![]() ,0),B(n+1+
,0),B(n+1+![]() ,0),
,0),
∵AM∥BN,
∴∠MAE=∠NBF,
∴Rt△AME∽Rt△BNF,
∴![]() ,即
,即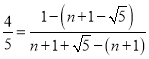 ,
,
∴n=![]() .
.



