题目内容
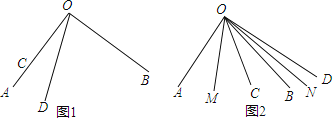
【题目】矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP=_____________.
【答案】1或4或9.
【解析】试题分析:首先根据题意画出图形,共分3种情况,画出图形后根据勾股定理即可算出DP的长.
解:(1)如图1,当AE=EP=5时,
过P作PM⊥AB,
∴∠PMB=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴四边形BCPM是矩形,
∴PM=BC=3,
∵PE=5,
∴EM=![]() =
=![]() =4,
=4,
∵E是AB中点,
∴BE=5,
∴BM=PC=5﹣4=1,
∴DP=10﹣1=9;
(2)如图2,当AE=AP=5时,DP=![]() =
=![]() =4;
=4;
(3)如图3,当AE=EP=5时,
过P作PF⊥AB,
∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,
∴四边形BCPF是矩形,
∴PF=AD=3,
∵PE=5,
∴EF=![]() =4,
=4,
∵E是AB中点,
∴AE=5,
∴DP=AF=5﹣4=1.
故答案为:1或4或9.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目