题目内容
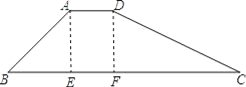
【题目】如图，在梯形ABCD中，AD∥BC，∠B=45°，AD=8，AB=
，CD=26，求BC的长．
【答案】42.
【解析】作AE⊥BC，DF⊥BC，垂足分别为E、F，由此可得出四边形AEFD是矩形，在Rt△ABE中利用勾股定理可求出AE的长，在Rt△DFC中利用勾股定理可求出FC的长，再根据线段之间的关系即可得出BC的长．
解：作AE⊥BC，DF⊥BC，垂足分别为E、F，如图所示．
∵AE⊥BC，DF⊥BC，
∴∠AEF=∠DFE=90°，AE∥DF．
∵AD∥BC，
∴四边形AEFD是矩形，
∴AE=DF，AD=EF=8．
在Rt△ABE中，由∠B=45°，得AE=BE
∴
，
∴AE=BE=10，
∴DF=10．
在Rt△DFC中，由DF=10，CD=26，
∴FC=
=24，
∴BC=BE+EF+FC=42．
“点睛”本题考查了条形的性质即直角三角形的性质，属于基础题，关键将作为的知识结合，做题时融会贯通.
练习册系列答案
智能训练练测考系列答案
相关题目
