题目内容
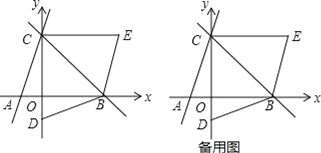
【题目】如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=﹣x+b与x轴交于点B.
(1)b的值为______;
(2)若点D的坐标为(0,﹣1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)3;(2)证明见解析;(3)存在,P1(4,-1),P2(2,1)
【解析】分析:(1)先由点C在直线y=3x+3上,求出点C坐标,代入直线y=-x+b中即可.(2)先求出∠OBC=∠OCB=45°,进而判断出CE∥AB,最后判断出CE=AB 即可;(3)方法①先确定出直线AD,BC解析式,进而判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可.
本题解析: (1)∵直线y=3x+3与x轴交于点A,与y轴交于点C,
∴C(0,3),
∵过点C的直线y=x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=1,
∴A(1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形。
(3)存在点P,使以P、A、 D、 B为顶点的四边形是平行四边形。
如图,

∵A(1,0)、D(0,1),
∴直线AD解析式为y=x1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,m+3),
∴![]() ,
,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴P(2,1)或P(4,1),
综上所述,存在点P,使以P、A、D、 B为顶点的四边形是平行四边形。点P的坐标为![]() (2,1)或
(2,1)或![]() (4,1).
(4,1).

