题目内容
【题目】如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.
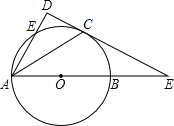
(1)求证:DC为⊙O切线;
(2)若DC=1,AC=![]() ,①求⊙O半径长;②求PB的长.
,①求⊙O半径长;②求PB的长.
【答案】(1)见解析;(2)⊙O半径长为![]() ;
;
【解析】
试题分析:(1)连结OC,如图,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于CD⊥AD,所以OC⊥CD,则根据切线的判定定理得到DC为⊙O切线;
(2)①连结BC,如图,在Rt△ACD中利用勾股定理计算出AD=2,再Rt△ACD∽Rt△ABC,利用相似比计算出AB=![]() ,从而得到⊙O半径长为
,从而得到⊙O半径长为![]() ;
;
②证明△EOC∽△EAD,然后利用相似比可计算出BE的长.
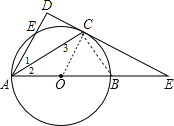
(1)证明:连结OC,如图,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥CD,
∴DC为⊙O切线;
(2)解:①连结BC,如图,
在Rt△ACD中,∵CD=1,AC=![]() ,
,
∴AD=![]() =2,
=2,
∵AB为直径,
∴∠ACB=90°,
∵∠1=∠2,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,即![]() :AB=2:
:AB=2:![]() ,
,
∴AB=![]() ,
,
∴⊙O半径长为![]() ;
;
②∵OC∥AD,
∴△EOC∽△EAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BE=![]() .
.

练习册系列答案
相关题目