题目内容
【题目】矩形![]() 中,
中, ![]() ,以
,以![]() 为边向上作正
为边向上作正![]() ,
, ![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,
, ![]() ,两动点
,两动点![]() 、
、![]() 运动速度分别为4
运动速度分别为4![]() 、
、![]() (
(![]() ).
).
(1)![]() 的长为
的长为 ![]() ;
;
(2)若点![]() 从
从![]() 出发沿线段
出发沿线段![]() 向
向![]() 运动,同时点
运动,同时点![]() 从
从![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 运动,设运动时间为
运动,设运动时间为![]() ,在运动过程中,以
,在运动过程中,以![]() 、
、![]() 、
、![]() 为顶点的三角形和以
为顶点的三角形和以![]() 、
、![]() 、
、![]() 为顶点的三角形全等,求
为顶点的三角形全等,求![]() 的运动速度
的运动速度![]() ;
;
(3)若点![]() 以(2)中的速度从点
以(2)中的速度从点![]() 出发,同时点
出发,同时点![]() 以原来的速度从点
以原来的速度从点![]() 出发,逆时针沿四边形
出发,逆时针沿四边形![]() 运动.问
运动.问![]() 、
、![]() 会不会相遇?若不相遇,说明理由.若相遇,请求出经过多长时间
会不会相遇?若不相遇,说明理由.若相遇,请求出经过多长时间![]() 、
、![]() 第一次在四边形
第一次在四边形![]() 的何处相遇?
的何处相遇?
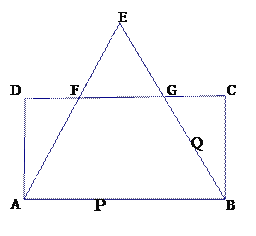
【答案】(1)AF=10cm;(2)![]() 或4cm\s;(3)5圈又运动了22cm后在BG边距点B 4cm处与点Q相遇.
或4cm\s;(3)5圈又运动了22cm后在BG边距点B 4cm处与点Q相遇.
【解析】试题分析:(1)先由△ABE是等边三角形,DF=5cm,求出FG的长,再由△EFG∽△EAB,对应边成比例求出AF的长;(2)先表示出AP、PB长,再由△AFP≌△BQP或△AFP≌△BPQ,
对应边相等列出方程解即可得到答案;(3)当Q的速度为V=4cm\s时,点P的速度也为4cm\s ,两点同向同速, 此时P,Q不会相遇;当Q的速度为V=![]() 时设经过xsP、
时设经过xsP、![]() 第一次相遇,根据题意得:
第一次相遇,根据题意得: ![]() ,即可得到经过63sP、
,即可得到经过63sP、![]() 第一次相遇.
第一次相遇.
试题解析:(1)∵△ABE是等边三角形,DF=5cm,
∴CG=5cm,∴FG=18-5-5=8cm,
∵FG∥AB,
△EFG∽△EAB,
∴![]() ,即
,即![]() ,
,
∴AF=10cm
(2)又题意得:AP=4t,PB=18-4t
①当△AFP≌△BPQ时,PB=AF 即:18-4t=10 ∴t=2s,此时:AP=4t=8cm=BQ,2V=8 ∴V=4cm\s
②当△AFP≌△BQP时,AF=BQ ,AP=PB,即:4t=18-4t
解得:t= ![]() ,
, ![]() 解得:V=
解得:V=![]()
(3)解:①当Q的速度为V=4cm\s时,因为点P的速度也为4cm\s ∴P,Q不会相遇
②当点Q的速度为V=![]() 时,∵
时,∵![]() >4cm\s
>4cm\s
∴点Q能追上点P
设:追上的时间为xs.又∵P,Q沿逆时针运动,Q 、P距离为28cm,
根据题意得: ![]() 解得:x=63s
解得:x=63s
又∵P的速度为4cm\s,∴P运动63s共走了: ![]()
而P从A出发逆时针,沿四边形ABGF的边运动,转一圈为46cm
∵46×5+22=252
∴P在沿四边形ABGF的边逆时针运动了5圈又运动了22cm后在BG边距点B 4cm处与点Q相遇(或距离点G6cm处与点Q相遇)

 百年学典课时学练测系列答案
百年学典课时学练测系列答案
