题目内容
9.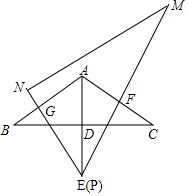 如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2$\sqrt{3}$,延长AD到E,使AE=2AD,连接BE.
如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2$\sqrt{3}$,延长AD到E,使AE=2AD,连接BE.(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.
分析 (1)先证明∠ABD=90°-∠BAE=30°,可知AB=2AD,由因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
(2)由(1)可知:∠ABE=∠AEB=60°,AE=BE,然后求证△BEG≌△AEF即可得出BG=AF;
(3)由于S四边形AGEF=S△AEG+S△AEF=S△AEG+S△BEG=S△ABE,故只需求出△ABE的面积即可.
解答 解:(1)AB=AC,AD⊥BC,
∴∠BAE=∠CAE=$\frac{1}{2}$BAC=60°,∠ADB=90°,
∴∠ABD=90°-∠BAE=30°,
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
∵∠BAE=60°,
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
∴∠ABE=∠AEB=60°,
AE=BE,
由(1)∠CAE=60°
∴∠ABE=∠CAE,
∵∠NEM=∠BEA=60°,
∴∠NEM-∠AEN=∠BEA-∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,
$\left\{\begin{array}{l}{∠GBE=∠FAE}\\{BE=AE}\\{∠BEG=∠AEF}\end{array}\right.$
∴△BEG≌△AEF(ASA)
∴BG=AF;
(3)由(2)可知:△BEG≌△AEF,
∴S△BEG=S△AEF,
∴S四边形AGEF=S△AEG+S△AEF
=S△AEG+S△BEG
=S△ABE
∵△ABE是等边三角形,
∴AE=AB=4,
∴S△ABE=$\frac{1}{2}$AE•BD=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
∴S四边形AGEF=4$\sqrt{3}$
点评 本题考查全等三角形的判定,涉及等边三角形的性质,三角形面积计算问题,综合程度较高.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 如图,将△ABC绕着点C顺时针旋转50°后得到△DEC.若∠A=40°,∠E=110°,则∠BCD的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△DEC.若∠A=40°,∠E=110°,则∠BCD的度数是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |
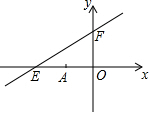 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形. 如图,AC=AD,BC=BD,求证:∠C=∠D.
如图,AC=AD,BC=BD,求证:∠C=∠D.