题目内容
19. 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形.(1)求函数y=$\frac{3}{4}$x+6的坐标三角形的三条边长;
(2)若函数y=$\frac{3}{4}$x+b(b为常数)的坐标三角形的周长为12,求此三角形的面积.
分析 (1)根据一次函数图象上点的坐标特征可求出点E、F的坐标,再利用勾股定理求出EF的长即可;
(2)根据一次函数图象上点的坐标特征可求出点E、F的坐标,结合勾股定理可求出EF的长,根据函数y=$\frac{3}{4}$x+b(b为常数)的坐标三角形的周长为12,即可求出|b|的值,代入三角形的面积公式即可得出结论.
解答 解:(1)当x=0时,y=6,
∴点F的坐标为(0,6),
∴OF=6;
当y=0时,$\frac{3}{4}$x+6=0,
解得:x=-8,
∴点E的坐标为(-8,0),
∴OE=8.
∴EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=10.
(2)当x=0时,y=b,
∴点F的坐标为(0,b),
∴OF=|b|;
当y=0时,$\frac{3}{4}$x+b=0,
解得:x=-$\frac{4}{3}$b,
∴点E的坐标为(-$\frac{4}{3}$b,0),
∴OE=$\frac{4}{3}$|b|.
∴EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=$\frac{5}{3}$|b|.
∵函数y=$\frac{3}{4}$x+b(b为常数)的坐标三角形的周长为12,
∴|b|+$\frac{4}{3}$|b|+$\frac{5}{3}$|b|=4|b|=12,
解得:|b|=3.
∴S△OEF=$\frac{1}{2}$•OE•OF=$\frac{1}{2}$×$\frac{4}{3}$|b|×|b|=$\frac{2}{3}$b2=6.
点评 本题考查了一次函数图象上点的坐标特征以及三角形的面积,根据一次函数图象上点的坐标特征找出点E、F的坐标是解题的关键.

练习册系列答案
相关题目
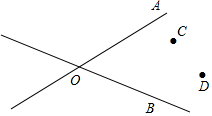 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)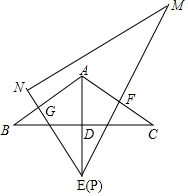 如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2$\sqrt{3}$,延长AD到E,使AE=2AD,连接BE.
如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2$\sqrt{3}$,延长AD到E,使AE=2AD,连接BE.