题目内容
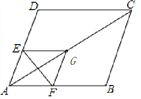
【题目】如图在菱形ABCD中,∠A=60°,AD=![]() ,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
,点P是对角线AC上的一个动点,过点P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为_________.
【答案】1或![]()
【解析】分析:首先证明四边形AEGF是菱形,分两种情形:①CG=CB,②GC=GB分别计算即可.
详解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=![]() ,∠DAC=∠BAC=
,∠DAC=∠BAC=![]()
![]() =30°,AC=3,如图,
=30°,AC=3,如图,
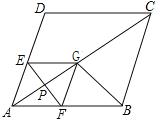
∵EF⊥AG,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EG,AF=FG,
∴AE=EG=GF=FA,
∴四边形AEGF是菱形,
∴AP=PG
①当CB=CG时,∵AG=AC-CG=3-![]() ,
,
∴AP=![]() AG=
AG=![]() .
.
②当GC=GB时,∵∠GCB=∠GBC=∠BAC,
∴△GCB∽△BAC,
∴![]() ,
,
∴GC=1,
∴AG=3-1=2,
∴AP=![]() AG=1.
AG=1.
故答案为1或![]() .
.

练习册系列答案
相关题目