Question

【题目】已知抛物线．

（1）求证：无论为任何实数，抛物线与轴总有两个交点；

（2）若A、B是抛物线上的两个不同点，求抛物线的表达式和的值；

（3）若反比例函数的图象与（2）中的抛物线在第一象限内的交点的横坐标为，且满足2<<3，求k的取值范围．

Answer 1

【答案】（2），（3）5＜k＜18

【解析】

试题分析：（1）根据抛物线的图像与性质可知其与x轴交点的判定条件是，因此可由判别式得证结果；

（2）根据题意可求得抛物线的对称轴，且有A，B的点可判断它们是对称点，根据对称性可求出m的值，求得抛物线的解析式，然后把A点的坐标代入解析式可求得n的值；

（3）根据二次函数的增减性以及反比例函数的图像与性质，可以判断出两函数之间的大小关系，构成不等式，从而解出k的取值范围．

试题解析：（1）证明：令．

得．

不论m为任何实数，都有（m－1）2＋3＞0，即△＞0．

∴不论m为任何实数，抛物线与x轴总有两个交点．

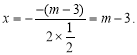（2）解：抛物线的对称轴为

∵抛物线上两个不同点A、B的纵坐标相同，

∴点A和点B关于抛物线的对称轴对称，则．

∴．

∴抛物线的解析式为．

∵A在抛物线上，

∴．

化简，得．

∴ ．

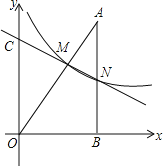
（3）当2<<3时，对于，y随着x的增大而增大，

对于，y随着x的增大而减小．

所以当时，由反比例函数图象在二次函数图象上方，得＞，

解得k＞5．

当时，由二次函数图象在反比例函数图象上方，得＞，

解得k＜18．

所以k的取值范围为5＜k＜18．