Question

【题目】（1）动手操作：

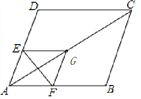
如图①，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点处，折痕为EF，若∠ABE=20°，那么的度数为 。

（2）观察发现：

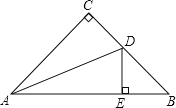
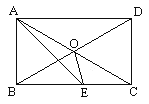
小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．

（3）实践与运用：

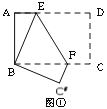
将矩形纸片ABCD 按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP=MN=PQ（如图④）,求∠MNF的大小。

Answer 1

【答案】（1）125°；（2）同意；（3）60°

【解析】

试题分析：（1）先根据矩形的性质结合三角形的内角和定理求得∠AEB的度数，再根据折叠的性质求得∠DEF的度数，然后根据平行线的性质求得∠EFC的度数，即可得到结果；

（2） 设AD与EF交于点G．由折叠的性质可得AD平分∠BAC，所以∠BAD=∠CAD．∠AGE=∠DGE=90°，即得∠AEF=∠AFE，从而可以证得结论；

（3）过N作NH⊥AD于H，设，根据折叠的性质及勾股定理可证得△MPF为等边三角形，则∠MFE=30°，∠MFN=60°，又MN=MF=，则△MNF为等边三角形，即可求得结果；

（1）因为∠ABE=20°，所以∠AEB=70°

由折叠知，∠DEF=55°

所以=∠EFC=125°；

（2）同意．

设AD与EF交于点G．

由折叠知，AD平分∠BAC，所以∠BAD=∠CAD．

由折叠知，∠AGE=∠DGE=90°，

所以∠AGE=∠AGF=90°，

所以∠AEF=∠AFE．所以AE=AF，

即△AEF为等腰三角形．

（3）过N作NH⊥AD于H

设

由折叠知， ①

②

∴△MPF为等边三角形

∴∠MFE=30°

∴∠MFN=60°，

又∵MN=MF=

∴△MNF为等边三角形

∴∠MNF=60°.