题目内容
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
【答案】C
【解析】
作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.利用待定系数法求出直线AB′的解析式,然后求出其与x轴交点的坐标,即M点的坐标.
如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
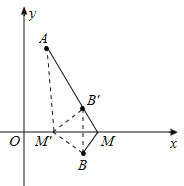
不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B′.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,
∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,3)和B′(3,1)代入得:
![]() ,
,
解之得
![]() ,
,
∴直线AB′解析式为y=-x+4.
令y=0,解得x=4,
∴M点坐标为(4,0).
故选:C.

练习册系列答案
相关题目
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.