题目内容
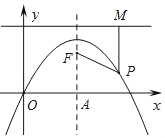
【题目】如图，抛物线y=﹣x2+2x的对称轴与x轴交于点A，点F在抛物线的对称轴上，且点F的纵坐标为
．过抛物线上一点P（m，n）向直线y=
作垂线，垂足为M，连结PF．
（1）当m=2时，求证：PF=PM；
（2）当点P为抛物线上任意一点时，PF=PM是否还成立？若成立，请给出证明；若不成立，请说明理由．
【答案】（1）证明见解析（2）点P为抛物线y=﹣x2+2x上任意一点都有PF=PM
【解析】试题分析：
当
时，求出
的值，此时点P为抛物线与
轴的右交点．求出
过点P作
于点B．分点B与点F重合和点B与点F不重合两种情况进行讨论.
试题解析：（1）当时，
∴此时点P为抛物线与轴的右交点．
垂直直线
的对称轴为直线x=1，点F的纵坐标为
在
中，
．
（2）
仍然成立．理由如下：
过点P作于点B．
当点B与点F重合时，
解得，
或
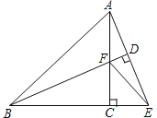
当点B与点F不重合时，如图．
在
中，
∵点
在抛物线上，
垂直直线 
综上，点P为抛物线
上任意一点都有．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．乐乐用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）增长或缩短．经测量，得到如下数据：
单层部分的长度（cm） | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度（cm） | … | 73 | 72 | 71 |
| … | 0 |
（1）根据上表中数据的规律，填写表格中空白处的数据；
（2）设单层部分的长度为xcm，请用含x的代数式表示出双层部分的长度 cm；
（3）根据乐乐的身高和习惯，挎带的长度为110cm时，背起来最舒适，请求出此时单层部分的长度．
