题目内容
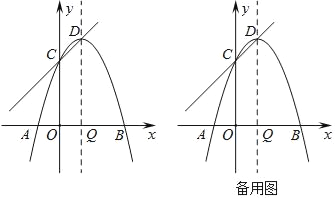
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).
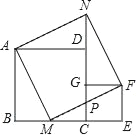
【答案】①②③.
【解析】
①根据正方形的性质得到∠BAD=∠ADC=∠B=90°,根据旋转的性质得到∴∠NAD=∠BAM,∠AND=∠AMB,根据余角的性质得到∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,可知∠DAM=∠AND,②根据旋转的性质得到GN=ME,等量代换得到AB=ME=NG,根据全等三角形的判定定理得到△ABM≌△NGF;③由旋转的性质得到AM=AN,NF=MF,根据全等三角形的性质得到AM=NF,推出四边形AMFN是矩形,根据余角的想知道的∠NAM=90°,推出四边形AMFN是正方形,于是得到S四边形AMFN=AM2=a2+b2;
①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,
∵将△ABM绕点A旋转至△ADN,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,
∴∠DAM=∠AND,故①正确,
②∵将△MEF绕点F旋转至△NGF,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在△ABM与△NGF中,AB=NG=a,∠B=∠NGF=90°,GF=BM=b,
∴△ABM≌△NGF;故②正确;
③∵将△ABM绕点A旋转至△ADN,
∴AM=AN,
∵将△MEF绕点F旋转至△NGF,
∴NF=MF,
∵△ABM≌△NGF,
∴AM=NF,
∴四边形AMFN是矩形,
∵∠BAM=∠NAD,
∴∠BAM+DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
∵在Rt△ABM中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故③正确
故答案为:①②③.

 习题精选系列答案
习题精选系列答案【题目】近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 | 频数/户 | 频率 |
0≤a<50 | 120 | 0.12 |
50≤a<100 | 240 | n |
100≤a<150 | 300 | 0.30 |
150≤a<200 | m | 0.16 |
200≤a<250 | 120 | 0.12 |
250≤a<300 | 60 | 0.06 |
合 计 | 1000 | 1 |
(1)频数分布表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.