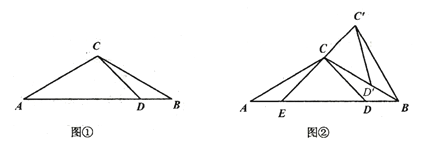
��Ŀ����
����Ŀ����ͼ����C���߶�![]() ��.��P�ӵ�C�������
��.��P�ӵ�C�������![]() �˶����ٶ�Ϊ2cm/s;ͬʱ����QҲ�ӵ�C��4cm/s�ٶȳ�����1s����A��������A��ͣ��2s��Ȼ��ԭ�ٶ����B�˶���.���գ���Q�ȵ�P��1s����B��.���P�˶���ʱ��Ϊt.
�˶����ٶ�Ϊ2cm/s;ͬʱ����QҲ�ӵ�C��4cm/s�ٶȳ�����1s����A��������A��ͣ��2s��Ȼ��ԭ�ٶ����B�˶���.���գ���Q�ȵ�P��1s����B��.���P�˶���ʱ��Ϊt.
(1)�߶�AC�ij�Ϊ cm;��t=3sʱ��P,Q����֮��ľ���Ϊ cm;
(2)���߶�BC�ij�;
(3)��P,Q����ͬʱ��������P�����B�������ʱ���ڣ�tΪ��ֵʱ��P,Q�������1cm��
![]()
���𰸡���1��4��10����2��BC=20�� (3) ![]()
��������
��1�����ݵ�C��4cm/s�ٶȳ�����1s����A�����ɼ�����߶�AC�ij�����t=3sʱ,��Q���ڵ�A�����������CP�ij����ɼ����P,Q����֮��ľ��룻
��2�����P�˶���ʱ��Ϊts�����Q��C�˶���B��ʱ��Ϊ��t-1-1-2-1��s,���������з��̼������t��ֵ��Ȼ�������߶�BC�ij�;
��3�����ݵ�P�͵�O���ٶȣ�����������ϵ�λ�ã���������ۣ����������з��̼������t��ֵ.
�⣺��1���ߵ�C��4cm/s�ٶȳ�����1s����A����
��AC=4��1=4,
���߶�AC�ij�Ϊ4cm��
�ߵ�t=3sʱ,��Q���ڵ�A��,PC=2��3=6,
��PQ=AC+CP=4+6=10,
�� P,Q����֮��ľ���Ϊ10cm.
(2) ���P�˶���ʱ��Ϊts�����Q��C�˶���B��ʱ��Ϊ��t-1-1-2-1��s,���������з��̵ã�2t=4(t-5),
��ã�t=10,
��BC=2��10=20
���߶�BC�ij�Ϊ20cm.
(3) �ٵ���Q��AC��ʱ�����������з��̵ã�4t+2t=1,
��ã�t= ![]() ;
;
�ڵ���Q��BC�����ڵ�P�����ʱ�����������з��̵ã�2t-4(t-4)=1,
��ã�t= ![]() ;
;
�۵���Q��BC�����ڵ�P���Ҳ�ʱ�����������з��̵ã�4(t-4)-2t=1,
��ã�t=![]() ;
;
�ܵ���Q�����B������P��δ����ʱ�����������з��̵ã�20-2t=1,
��ã�t= ![]() ,
,
������������tΪ��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ʱ��P,Q�������1cm.
ʱ��P,Q�������1cm.