题目内容
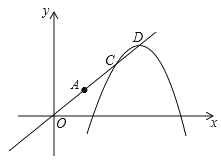
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与轴负半轴交于点
的左侧),与轴负半轴交于点![]() ,若
,若![]() .
.
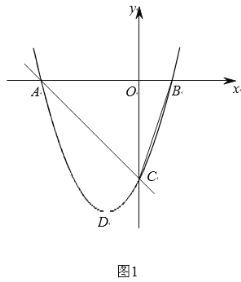
(1)求抛物线的解析式;
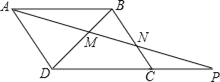
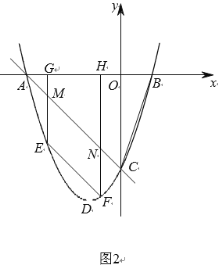
(2)如图2,![]() 是第三象限内抛物线上的动点,过点
是第三象限内抛物线上的动点,过点![]() 交抛物线于点
交抛物线于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,当四边形
,当四边形![]() 的周长最大值时,求点
的周长最大值时,求点![]() 的横坐标;
的横坐标;
(3)在![]() 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点
为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)x2(a+1)x+a=0,则AB=![]() =(a1)2=16,即可求解;
=(a1)2=16,即可求解;
(2)设点E(m,m2+2m3),点F(3m,m2+4m),四边形EMNF的周长S=ME+MN+EF+FN,即可求解;
(3)分当点Q在第三象限、点Q在第四象限两种情况,分别求解即可.
解:(1)x2(a+1)x+a=0,
则x1+x2=a+1,x1x2=a, AB=![]() =(a1)2=16,
=(a1)2=16,
解得:a=5或3,
抛物线与y轴负半轴交于点C,故a=5舍去,则a=3,
则抛物线的表达式为:y=x2+2x3;
(2)由y=x2+2x3得:点A、B、C的坐标分别为:(3,0)、(1,0)、(0,3),
设点E(m,m2+2m3),OA=OC,故直线AC的倾斜角为45°,EF//AC,
直线AC的表达式为:y=x3,
则设直线EF的表达式为:y=x+b,将点E的坐标代入上式并解得:
直线EF的表达式为:y=x+(m2+3m3)
联立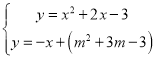 并解得:x=m或3m,
并解得:x=m或3m,
故点F(3m,m2+4m),点M、N的坐标分别为:(m,m3)、(3m,m+3),
则EF=![]() (xFxE)=
(xFxE)= ![]() (2m3)=MN,
(2m3)=MN,
四边形EMNF的周长S=ME+MN+EF+FN=2m2(6+4![]() )m6
)m6![]() ,
,
∵2<0,故S有最大值,此时m=![]() ,
,
故点E的横坐标为-![]() ;
;
(3)①当点Q在第三象限时,
当QC平分四边形面积时,
则|xQ|=xB=1,故点Q(1,4);
当BQ平分四边形面积时,
则S△OBQ= ![]() ×1×|yQ|,S四边形QCBO=
×1×|yQ|,S四边形QCBO=![]() ×1×3+
×1×3+![]() ×3×|xQ|,
×3×|xQ|,
则2(![]() ×1×|yQ|)=
×1×|yQ|)=![]() ×1×3+
×1×3+![]() ×3×|xQ|,
×3×|xQ|,
解得:xQ=![]() ,故点Q(
,故点Q(![]() ,
,![]() );
);
②当点Q在第四象限时,
同理可得:点Q(![]() ,
,![]() );
);
综上,点Q的坐标为:(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 优学名师名题系列答案
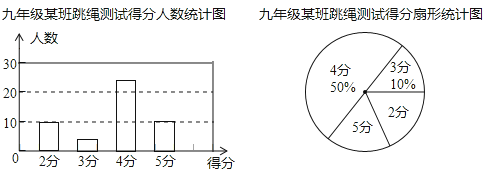
优学名师名题系列答案【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
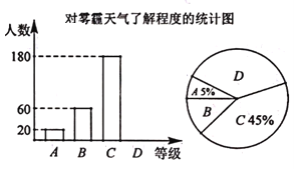
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).