题目内容
【题目】将连续奇数1,3,5,7,9,……排成如下的数表：
……………
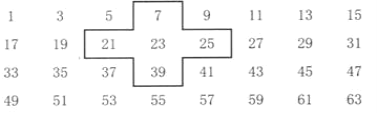
(1)设中间的数为a,求这十字框中五个数之和（请用含字母a的代数式表示）；
(2)将十字框上、下、左、右平移，可框住另外五个数，这五个数还有这种规律吗？
(3)十字框中的五个数的和能等于2015吗？若能，请求出这五个数；若不能，说明理由。那么2012呢？
【答案】（1）5a;（2）有;（3）能，387、401、403、405、419；不能，5a
2012.
【解析】
（1）根据框中的五个数的关系（竖着相邻两数差16，横着相邻两数差2），分别用a表示出其它的四个数，求和即可；
（2）假设中间数为x，再利用（1）的求法说明规律仍然成立即可；
（3）由（2）中得到的规律，利用五个数的和列方程，若能求出奇数a，则能，并求出这五个数即可；若求出的a不是奇数，则不能.
解：（1）根据题意：中间的数为a,则上边的数为（a－16），左边的数为（a－2），右边的数为（a＋2），下边的数为（a＋16），五个数的和为：
（a－16）+（a－2）+a+（a＋2）+（a＋16）=5a
（2）有，理由如下：
设中间数为x，则上边的数为（x－16），左边的数为（x－2），右边的数为（x＋2），下边的数为（x＋16），五个数的和为：
（x－16）+（x－2）+x+（x＋2）+（x＋16）=5x，故可得结论：十字框中的五个数的和恒等于中间数的5倍.
（3）由（2）中的结论，若十字框中的五个数的和等于2015
5a=2015
解得：a=403，符合题意
则这五个数分别是：387、401、403、405、419；
若十字框中的五个数的和等于2012
5a=2012
a=402.4，不符合题意，故不能.
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
