题目内容
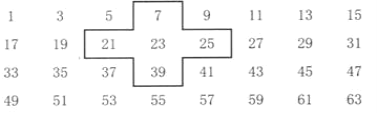
【题目】若用点A,B,C分别表示有理数a,b,c,它们在数轴上的位置如图所示.
![]()
(1)比较a,b,c的大小(用“<”连接);
(2)请在横线上填上>,< 或 =:a+b____ 0 , b-c____ 0;
(3)化简:2c+|a+b|+|c-b|-|c-a|.
【答案】(1)a<c<b;(2)< ;>;(3)0.
【解析】
(1)利用数轴上的数从左至右逐渐变大比较即可;
(2)根据有理数的加法法则和减法法则判断即可;
(3)根据绝对值的非负性去绝对值,并合并同类项即可.
解:(1)由数轴上的数从左至右逐渐变大可知:a<c<b;
(2)由数轴可知:a<0,b>0,且![]()
根据有理数的加法法则:异号相加,取绝对值大的符号
故a+b<0;
根据减法法则:减去一个数等于加上它的相反数,得:b-c=b+(-c)
由数轴可知:b>0,(-c)>0,属于同号相加,符号不变
故b-c>0;
(3)由数轴可知:a+b<0,c-b<0,c-a>0,
所以2c+|a+b|+|c-b|-|c-a|
=2c-a-b-c+b-c+a
=0

练习册系列答案
相关题目
【题目】某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据:
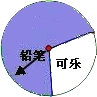
(1)计算并完成表格:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的频率m/n | 0.68 | 0.74 | △ | 0.69 | 0.705 | △ |
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)