题目内容
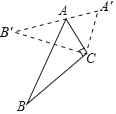
【题目】如图，△ABC中，∠ACB＝90°，∠ABC＝25°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为（ ）
A. 65°B. 60°C. 50°D. 40°
【答案】C
【解析】
先利用互余计算出∠BAC＝65°，再利用旋转的性质得CA＝CA′，∠A′＝∠A′AC＝65°，∠ACA′等于旋转角，根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可．
解：∵∠ACB＝90°，∠ABC＝25°，
∴∠BAC＝65°，
∵以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，
∴CA＝CA′，∠A′＝∠BAC＝65°，∠ACA′等于旋转角，
∴∠CAA′＝∠A′＝65°，
∴∠ACA′＝180°﹣65°﹣65°＝50°，
即旋转角的度数为50°．
故选：C．
练习册系列答案
相关题目
