题目内容
【题目】如图,等边△ABC的边长为2,CD为AB边上的中线,E为线段CD上的动点,以BE为边,在BE左侧作等边△BEF,连接DF,则DF的最小值为_____.

【答案】![]()
【解析】
连接AF,由等边三角形的性质可证△ABF≌△CBE,可得∠BAF=∠BCE=30°,即当DF⊥AF时,DF的值最小,由直角三角形的性质可求DF的最小值.
解:如图,连接AF,

∵△ABC是等边三角形,CD为AB边上的中线,
∴AB=BC=2,AD=BD=1,∠ABC=∠ACB=60°,∠BCE=30°,
∵△BEF是等边三角形
∴BF=BE,∠FBE=60°
∴∠FBE=∠ABC,
∴∠ABF=∠CBE,且AB=BC,BF=BE,
∴△ABF≌△CBE(SAS)
∴∠BAF=∠BCE=30°,
∴当DF⊥AF时,DF的值最小,
此时,∠AFD=90°,∠FAB=30°,
∴AD=2DF
∴DF的最小值为![]()
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
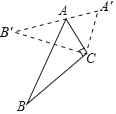
A. 65°B. 60°C. 50°D. 40°
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?



