题目内容
【题目】已知动点P以2cm/s的速度沿如图所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S (cm2), S与运动时间t (s)的关系如图所示,若AB=6cm,请回答下列问题:
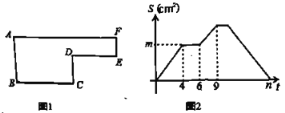
(1)如图中BC=______cm, CD=______cm,DE=______cm
(2)求出如图中边框所围成图形的面积;
(3)求如图中m、n的值;
(4)分别求出当点P在线段BC和DE上运动时S与t的关系式,并写出t的取值范围.
【答案】(1) 8,4,6;(2) 60cm2;(3) m=24cm2,n=17s;(4) 当点P在BC上运动上运动时,即0<t≤4时,s=6t.当点P在DE上运动时,即6≤t≤9时,s=6t-12.
【解析】
(1)根据路程=速度×时间,即可解决问题.
(2)根据矩形的面积公式计算即可;
(3)由上图可知m的值就是△ABC面积,n的值就是运动的总时间,由此即可解决.
(4)分两种情形分别求解即可解决问题;
解:(1)已知当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,由第二个图得,P在BC上移动了4秒,那么BC=4×2=8cm.在CD上移动了2秒,CD=2×2=4cm,在DE上移动了3秒,DE=3×2=6cm,而AB=6cm,那么EF=AB-CD=2cm,
故答案是:8;4;6;
(2) 由图可知,BC=4×2=8cm,CD=(6-4)×2=4cm,DE=(9-6)×2=6cm,AB=6cm,
∴AF=BC+DE=14cm,
∴图1的面积是:ABAF-CDDE=6×14-4×6=84-24=60cm2;
(3)由图得,m是点P运行4秒时△ABP的面积,∴S△ABP=![]() ×6×8=24.
×6×8=24.
n为点P走完全程的时间为:t=9+1+7=17s,
∴m=24,n=17.;
(4)当点P在BC上运动上运动时,即0<t≤4时,s=![]() ×6×2t=6t.
×6×2t=6t.
当点P在DE上运动时,即6≤t≤9时,s=![]() ×6×[8+2(t-6)]= 6t-12.
×6×[8+2(t-6)]= 6t-12.

 黄冈创优卷系列答案
黄冈创优卷系列答案