��Ŀ����
����Ŀ��ȥѧУʳ�þͲͣ���������һ����˴���ǰ�ȴ��������鷢�֣�ͬѧ�����ʶ�ָ��y���ʱ��x���֣�֮�����㷴����������ϵ�����±���
�ȴ�ʱ��x | 1 | 2 | 5 | 10 | 20 |
���ʶ�ָ��y | 100 | 50 | 20 | 10 | 5 |
��֪ѧ���ȴ�ʱ�䲻����30����
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�����ȴ�ʱ��8����ʱ�������ʶȵ�ֵ��
��3�����ʶ�ָ��������10ʱ��ͬѧ�Ż�е����ʣ���˵������Ϊʳ�õĹ���Ա����ÿ���ڴ�����˵�ͬѧ���ȴ�����ʱ�䣿
���𰸡�(1)y=![]() ��0��x��30��;(2)12.5;(3) ���ȴ�10����.
��0��x��30��;(2)12.5;(3) ���ȴ�10����.
���������������: ��1���۲�����֣�1��100=2��50=5��20���Ӷ�ȷ��������ϵʽy=![]() ��y�������ʶ�ָ����x���֣������ȴ�ʱ�䣮
��y�������ʶ�ָ����x���֣������ȴ�ʱ�䣮
��2������֪x=8�����뺯������ʽ���y��
��3������֪y��10���Ϳ��Եõ�����x�IJ���ʽ���x�ķ�Χ��
�������:
��1���۲�����֣�1��100=2��50=5��20=����
��xy=100��
��y=![]() ��0��x��30����
��0��x��30����
��2����x=8ʱ�����ʶ�y=![]() =12.5��
=12.5��
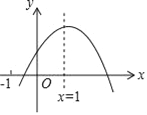
��3�����ʶ�ָ��������10ʱ����ͼ��y��10ʱ��0��x��10
������Ϊʳ�õĹ���Ա����ÿ���ڴ�����˵�ͬѧ���ȴ�10���ӣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ