题目内容
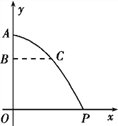
【题目】已知在△ABC和△ABD中,∠DAB=∠ABC=90°,AD=AB=CB,BD=6cm,F为线段BD上一动点,以每秒1cm的速度从B匀速运动到D,过F作直线FQ⊥AF,且FQ=AF,点Q在直线AF的右侧,设点F运动时间为t(s).
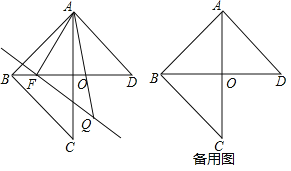
(1)当△ABF为等腰三角形时,t= ;
(2)当F点在线段BO上时,过Q点作QH⊥BD于点H,求证:△AOF≌△FHQ;
(3)当F点在线段OD上运动的过程中,△ABQ的面积是否变化?若不变,求出它的值.
【答案】(1)3s或6s;(2)见解析;(3)不变,9.
【解析】
(1)分两种情况讨论,由等腰三角形的性质可求BF的长,即可求t的值;
(2)由等腰三角形的性质可得∠AOB=90°,由“AAS”可证△AOF≌△FHQ;
(3)由“AAS”可证△AOF≌△FHQ,可得OF=QH=t﹣3,由面积的和差关系可求解.
解:(1)∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
若AB=AF时,即点F与点D重合,
∴BF=BD=6cm,
∴t=![]() =6s,
=6s,
若BF=AF时,
∴∠ABF=∠BAF=45°,
∴∠AFB=90°,
∴AF⊥BD,且AB=AD
∴BF=DF=3cm,
∴t=![]() =3s,
=3s,
故答案为:3s或6s;
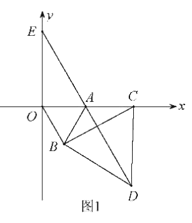
(2)如图1,
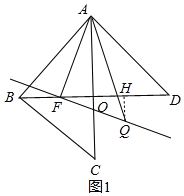
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS);
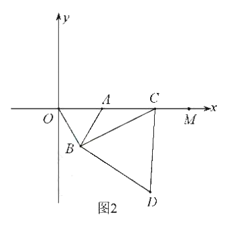
(3)不变,
理由如下:如图2,过点Q作QH⊥BD,
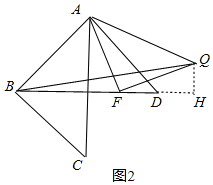
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS)
∴OF=QH=t﹣3,
∵S△ABQ=S△AOF+S△AFQ﹣S△BFQ=![]() BF×AO+
BF×AO+![]() ×AF2﹣
×AF2﹣![]() ×BF×QH,
×BF×QH,
∴S△ABQ=![]() ×t×3+
×t×3+![]() [32+(t﹣3)2]﹣
[32+(t﹣3)2]﹣![]() ×t×(t﹣3)=9,
×t×(t﹣3)=9,
故△ABQ的面积不发生变化.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】银川九中要举办“不忘初心跟党走”2018年元旦合唱比赛,为迎接比赛,某校区七年级(3)(4)班决定订购同一套服装,两班一共有103人(三班人数多于四班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么三、四班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
(3)该服装店此次出售的服装每套成本是32元,如果按上面的第(2)问形式购买,请计算这个服装店此次出售服装的利润率是多少?