��Ŀ����
����Ŀ����֪����Rt��ABC�У���C=90����A����B����C���Եı߷ֱ����a��b��c��
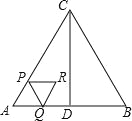
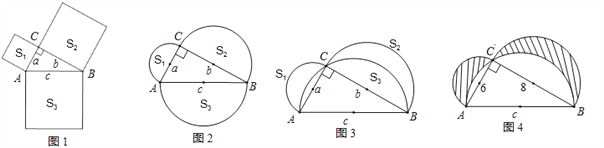
��1����ͼ1���ֱ�����ABC��������Ϊ�߳������������Σ��������ε������С����ֱ����S1��S2��S3������____________��
��2����ͼ2���ֱ�����ABC��������Ϊֱ����������Բ�����Բ�������С����ֱ����S1��S2��S3������S1+S2��S3��������������ϵ����֤����Ľ��ۣ�
��3���ֱ���ֱ�������ε�������Ϊֱ������Բ����ͼ3��ʾ���������С����ֱ����S1��S2��S3�����ݣ�2���е�̽����ֱ�ӻش�S1+S2��S3��������������ϵ��
��4����Rt��ABC�У�AC=6��BC=8�����ͼ4����Ӱ���ֵ������
���𰸡�(1)S1+S2=S3����2��![]() ����3��
����3��![]() ��(4)24cm
��(4)24cm![]() .
.
�������������������1�����ݹ��ɶ������ɵõ�a��b��c����Ĺ�ϵ��
��2�����������ε������ʽ��Ϲ��ɶ����Ϳɷ��ִ������ε����������С�����ε�����ͣ�
��3���ֱ��ʾ��S1��S2��S3����Ϲ��ɶ������ɵó���ϵʽ��
��4�����ݰ�Բ�������ʽ�Լ����ɶ����Ϳɷ��֣�����С��Բ������͵��ڴ��Բ��������Ӷ��ó���Ӱ���ֵ����=ֱ�������ε������
�����������1�����ݹ��ɶ����ɵ�S1+S2=S3��
��2��������ã�S1=b2��S2=a2��S3=c2����a2+b2=c2����S1+S2=S3��
��3��S1=![]() ��b2��S2=
��b2��S2=![]() ��a2��S3=
��a2��S3=![]() ��c2����a2+b2=c2����S1+S2=S3��
��c2����a2+b2=c2����S1+S2=S3��
��4����Ϊa2+b2=c2������ͬ����![]() ��������С��Բ������͵��ڴ��Բ�������
��������С��Բ������͵��ڴ��Բ�������
�Ӷ��ɵ�S��Ӱ���ֵ����=Sֱ�������ε����=![]() ��8��6=24������Ӱ���ֵ������24��
��8��6=24������Ӱ���ֵ������24��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д�����Ŀ��Ϊѡ��һ��ѧ���μ�ȫ��ʵ������ܾ�����A.B��λͬѧ��ѧУʵϰ�����ֳ����мӹ�ֱ��Ϊ20mm������IJ��ԣ��������ӹ���10����������������������ͼ����ʾ����λ��mm��
ƽ���� | ���� | ��ȫ����Ҫ����� | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
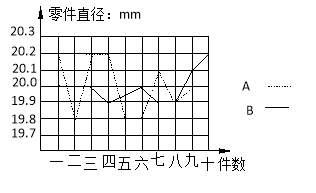
���ݲ��Եõ����й����ݣ��Խ���������⣺
�� ����ƽ��������ȫ����Ҫ��ĸ���������Ϊ �ijɼ���Щ��
�� �����SB2�Ĵ�С������ƽ�����뷽�˵��˭�ijɼ���Щ��
�� ����ͼ���������Ƽ������мӹ��������ԶԶ����10����ʵ�����������Ϊ��˭ȥ�����Ϻ��ʣ�˵��������ɡ�
����Ŀ��2015��3��3�յ�3��15�գ������ھ����Σ��������������ܵ�������ձ��ע��ij��������ԡ����������������ע�Ļ�����ʲô��Ϊ���⣬ͨ����ͷ��ú�����������ַ�ʽ���е��飬���ݵ����������ݻ����˱���
���ע�Ļ��� | ��ͷ���/�� | �������/�� | �ϼ�/�� |
������ʲô | 120 | 200 | |
�������� | 40%a | 60%a | a |
���������ҷ������� | 600 | ||
�������� | 60 |
��1���μӱ��ν�ͷ��ú����������������Ƕ����ˣ�a��ֵΪ������
��2�����㽫���ϱ����пհ״�����������
��3�����ڽ��ܽ�ͷ��õ���Ա��������һ�ˣ���鵽���ע�����������ҷ������ԡ���Ա�ĸ����ǡ����٣�����