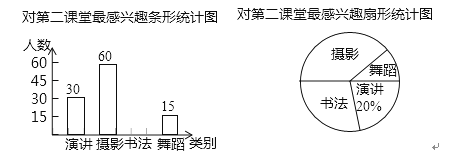
��Ŀ����
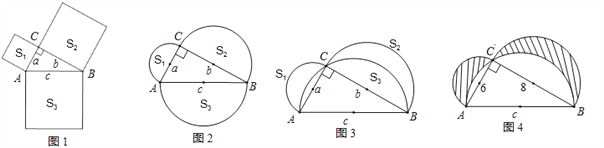
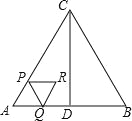
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4cm��CD��AB�ڵ�D������P�ӵ�A��������AC��2cm/s���ٶ����յ�C�˶�������P��������P��PQ��BC������AD��DC�ڵ�Q����PQΪ�����ȱ�������PQR�����ı���APRQ����ACD�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����
��1������Q���߶�AD��ʱ���ú�t�Ĵ���ʽ��ʾQR�ij���
��2�����R�˶���·�̳���
��3������Q���߶�AD��ʱ����S��t֮��ĺ�����ϵʽ��
��4��ֱ��д���Ե�B��Q��RΪ�������������ֱ��������ʱt��ֵ��
���𰸡���1��֤����������2��2![]() +2��3����S=S����APRQ2
+2��3����S=S����APRQ2![]() t2����S=��
t2����S=��![]() t2+6
t2+6![]() t��2
t��2![]() ��4��t=
��4��t=![]() ��t=
��t=![]()
��������
�����������1����֤��APQ�ǵȱ������Σ����ɵõ�QR=PQ=AP=2t��
��2������A��AG��BC�ڵ�G����ͼ�ڣ��õ�R�˶���·�̳���AG+CG��ֻ�����AG��CG�Ϳɽ�����⣻
��3���ı���APRQ����ACD�ص�����ͼ�ο��������Σ�Ҳ����������Σ������������ۣ�Ȼ�����ø���Ϳɽ�����⣻
��4������ֱ�Ƕ��㲻ȷ���������������ۣ�ֻ�����QRB=90�����RQB=90������������ۣ����ɽ�����⣮
�����������1����ͼ�٣�

�ߡ�ABC�ǵȱ������Σ�
���ACB=��B=60�㣮
��PQ��BC��
���APQ=��ACB=60�㣬��AQP=��B=60�㣬
���APQ�ǵȱ������Σ�
��PQ=AP=2t��
�ߡ�PQR�ǵȱ������Σ�
��QR=PQ=2t��
��2������A��AG��BC�ڵ�G����ͼ�ڣ�

���R�˶���·�̳���AG+CG��
��Rt��AGC�У���AGC=90�㣬sin60��=![]() ��cos60��=
��cos60��=![]() ��AC=4��
��AC=4��
��AG=2![]() ��CG=2��
��CG=2��
����R�˶���·�̳�2![]() +2��
+2��
��3���ٵ�0��t��![]() ʱ����ͼ�ۣ�
ʱ����ͼ�ۣ�

S=S����APRQ=2��S����APQ=2��![]() ����2t��2=2
����2t��2=2![]() t2��
t2��
�ڵ�![]() ��t��1ʱ����ͼ��
��t��1ʱ����ͼ��

PE=PCsin��PCE=��4��2t����![]() =2��t��
=2��t��
��ER=PR��PE=2t����2��t��=3t��2��
��EF=ERtanR=![]() ��3t��2��
��3t��2��
��S=S����APRQ��S��REF
=2![]() t2��
t2��![]() ��3t��2��2=��
��3t��2��2=��![]() t2+6
t2+6![]() t��2
t��2![]() ��
��
��4��t=![]() ��t=
��t=![]()
��ʾ���ٵ���QRB=90��ʱ����ͼ�ݣ�

cos��RQB=![]() ��
��
��QB=2QR=2QA��
��AB=3QA=6t=4��
��t=![]() ��
��
�ڵ���RQB=90��ʱ����ͼ�ޣ�

ͬ���ɵ�BC=3RC=3PC=3��4��2t��=4��
��t=![]() ��
��

����Ŀ��ijУ����Ƹһ����ѧ��ʦ��ѧУ�Լס��ҡ�����λ��ѡ�˽����������������ԣ�������Գɼ����־�Ϊ100�֣����ݽ������¼�ã���λ��ѡ�˵ĸ�����Գɼ����±���ʾ��
������Ŀ | |||
���Գɼ�/�� | |||
�� | �� | �� | |
��ѧ���� | 85 | 73 | 73 |
�������� | 70 | 71 | 65 |
��֯���� | 64 | 72 | 84 |
(1)�������������Ե�ƽ���ɼ���˭����¼�ã�˵�����ɣ�
(2)����ʵ����Ҫ��ѧУ����ѧ�����к���֯�����������Ե÷ְ�5��3��2�ı���ȷ��ÿ�˵ijɼ���˭����¼�ã�˵�����ɣ�