题目内容
【题目】2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
雾霾是什么 | 120 | 200 | |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 600 | ||
其他话题 | 60 |
(1)参加本次街头随访和网络调查的总人数是多少人,a的值为多少;
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 多少? ;
【答案】解:(1)参加本次街头随访和网络调查的总人数是 2000人,a的值为 300;
(2)请你将以上表格中空白处补充完整;
街头随访/人 | 网络调查/人 | 合计/人 | |
雾霾是什么 | 80 | 120 | 200 |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 800 | 600 | 1400 |
其他话题 | 40 | 60 | 100 |
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 ![]() ;
;
【解析】(1)根据关注雾霾是什么的人数除以关注雾霾是什么所占的比例,可得调查总人数,根据调查总人数乘以雾霾治理所占的百分比,可得答案;
(2)根据调查总人数乘以雾霾自我防护策略所占的百分比,可得相应的人数,根据有理数的减法,可得其他话题人数,可得答案;
(3)根据街头随访中“雾霾自我防护策略的人数”除以街头随访的人数,可得答案;
【考点精析】本题主要考查了扇形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能正确解答此题.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图. 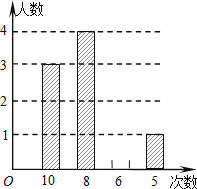
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a=;
(2)请将条形统计图补充完整;