题目内容
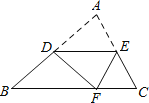
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

【答案】(1)见解析;(2)见解析;(3)4![]()
【解析】试题分析:(1)先证明![]() ,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
(2)由(1)可知: ![]() AE=BE,然后求证
AE=BE,然后求证![]() 即可得出BG=AF;
即可得出BG=AF;
(3)由于∴S四边形![]() 故只需求出△ABE的面积即可.
故只需求出△ABE的面积即可.
试题解析:
(1)AB=AC,AD⊥BC,
![]()
![]()
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
![]()
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
![]()
AE=BE,
由(1) ![]()
∴∠ABE=∠CAE,
![]()
∴∠NEM∠AEN=∠BEA∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,

![]()
∴BG=AF;
(3)由(2)可知: ![]()
![]()
∴S四边形![]()
∵△ABE是等边三角形,
∴AE=AB=4,
![]()
∴S四边形![]()

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目