题目内容
【题目】如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC.
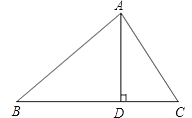
(1)求证:AC=BD;
(2)若sin∠C=![]() ,BC=12,求AD的长.
,BC=12,求AD的长.
【答案】(1)证明见解析(2)8
【解析】试题分析:(1)由于tanB=cos∠DAC,所以根据正切和余弦的概念证明AC=BD;
(2)设AD=12k,AC=13k,然后利用题目已知条件解直角三角形即可.
试题解析:解:(1)∵AD是BC上的高,∴AD⊥BC,∴∠ADB=90°,∠ADC=90°.在Rt△ABD和Rt△ADC中,∵tanB=![]() ,cos∠DAC=
,cos∠DAC=![]() ,tanB=cos∠DAC,∴
,tanB=cos∠DAC,∴![]() =
=![]() ,∴AC=BD.
,∴AC=BD.
(2)在Rt△ADC中,sinC=![]() ,故可设AD=12k,AC=13k,∴CD=
,故可设AD=12k,AC=13k,∴CD=![]() =5k,∵BC=BD+CD,AC=BD,∴BC=13k+5k=18k.由已知BC=12,∴18k=12,∴k=
=5k,∵BC=BD+CD,AC=BD,∴BC=13k+5k=18k.由已知BC=12,∴18k=12,∴k=![]() ,∴AD=12k=12×
,∴AD=12k=12×![]() =8.
=8.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.






