题目内容
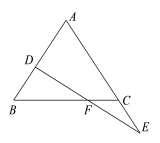
【题目】如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，BE、CD相交于点O.
（1）若BD=CE，试说明：OB=OC.
（2）若BC=10，BC边上的中线AM=12，试求AC的长.
【答案】（1）理由见试题解析；（2）13．
【解析】
（1）先根据边角边证明两三角形全等，然后利用全等三角形的性质得到∠OBC=∠OCB，在用等角对等边得到OB=OC．
（2）根据等腰三角形的性质得到AM是BC的垂直平分线，然后在直角△ACM中用勾股定理计算求出AC的长．
（1）∵AB=AC，
∴∠ABC=∠ACB，
又∵BD=CE，BC=CB，
∴△DBC≌△ECB，
∴∠DCB=∠EBC，∴OB=OC；
（2）由等腰三角形“三线合一”可得AM⊥BC且CM=
BC=5，
在Rt△AMC中，AC=
．
练习册系列答案
相关题目
【题目】为了促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中折线反映了每户每月用电电费y（元）与用电量x（度）间的函数关系式．
（1）根据图象，阶梯电价方案分为三个档次，填写下表：
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x（度） | 0＜x≤140 |
（2）小明家某月用电120度，需交电费 元
（3）求第二档每月电费y（元）与用电量x（度）之间的函数关系式；
（4）在每月用电量超过230度时，每多用1度电要比第二档多付电费m元，小刚家某月用电290度，交电费153元，求m的值．
