题目内容
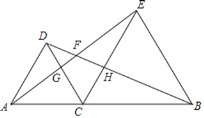
【题目】已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.
(1)求证:△ACE≌△DCB;
(2)求∠AFB的度数.
【答案】(1)见解析;(2)∠AFB=120°.
【解析】
(1)因为△DAC和△ECB均为等边三角形,则有AC=DC,CE=CB,∠ACD=∠ECB=60°,然后求出∠ACE=∠DCB,利用SAS即可证得△ACE≌△DCB;
(2)由全等三角形的性质和三角形内角和定理可得出结果.
解:(1)∵△DAC是等边三角形,
∴AC=DC,∠ACD=60°,
∵△BCE是等边三角形,
∴CE=CB,∠ECB=60°,
∴∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△BCD中,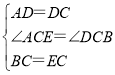 ,
,
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠AEC=∠DBC,
又∵∠EHF=∠BHC,
∴∠EFH=∠BCH=60°,
∴∠AFB=180°60°=120°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.