题目内容
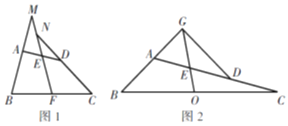
【题目】(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
【答案】(1)证明见解析;(2)OE=![]() .
.
【解析】
(1)连结BD,取DB的中点H,连结EH、FH,证明出EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,证出HE=HF,进而证出AB=CD;
CD,证出HE=HF,进而证出AB=CD;
(2)连结BD,取DB的中点H,连结EH、OH,证明出HO=HE,可证明证出△OEH是等边三角形,进而求出OE=![]() .
.
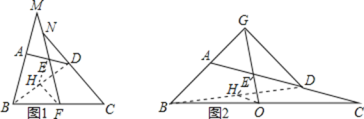
(1) 证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=![]() AB,FH∥CD,FH=
AB,FH∥CD,FH=![]() CD,
CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2) 如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=![]() AB=
AB=![]() CD,,
CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=![]() .
.
故答案为:(1)证明见解析;(2)OE=![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
【题目】点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 | 0 | 2 | 4 | 6 | 8 | 10 |
h/厘米 | 30 | 29 | 28 | 27 | 26 | 25 |
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式_____;这根蜡烛最多能燃烧的时间为_____分.